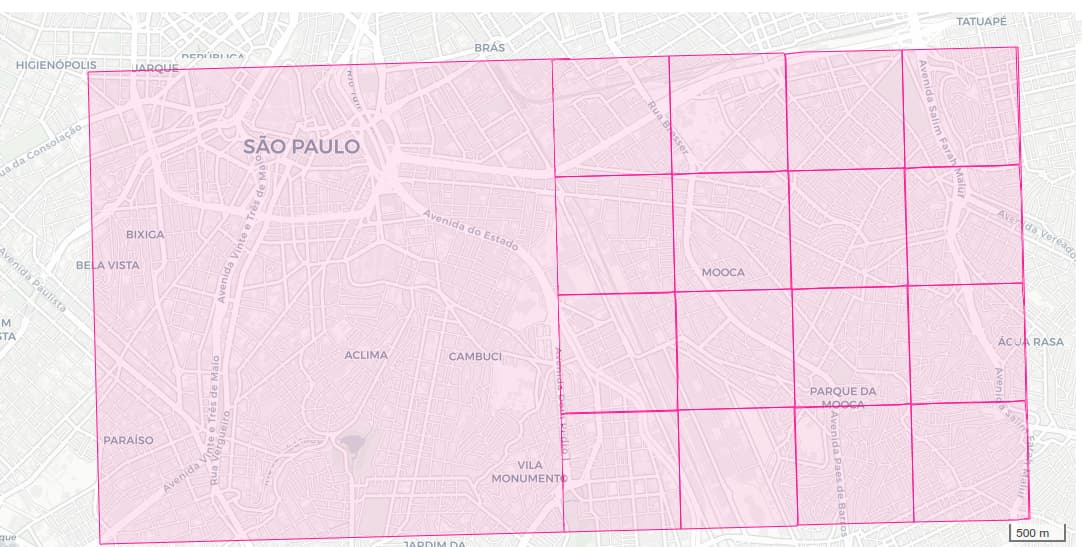
Grades estatísticas são convenções locais de cada nação: é uma boa prática garantir a interoperabilidade de dados espaciais do país, caberia ao governo exigir que dados por exemplo do Censo, do Meio Ambiente e da Fazenda sejam publicados neste tipo de grade padronizada.
Matematicamente a grade estatística pode ser imaginada como um mosaico de ladrilhos quase idênticos (igual área) recobrindo o território nacional. Podem ser triângulos, quadradados ou hexágonos.
A maioria das convenções desse tipo abrange mais de uma escala, ou seja, cada ladrilho do mosaico pode ser subdividido ele mesmo numa pequena sub-grade, resultando num conjunto hierárquico de grades com ladrilhos cada vez menores, contidos exatamente nos ladrilhos do nível anterior.
As grades nacionais tentam encaixar o mapa do país numa caixa. Imaginando uma caixa quadrada, veremos a hierarquia surgir de sucessivas partições desse quadrado original de lado h0 em quadrados menores, compondo grades mais e mais refinadas:
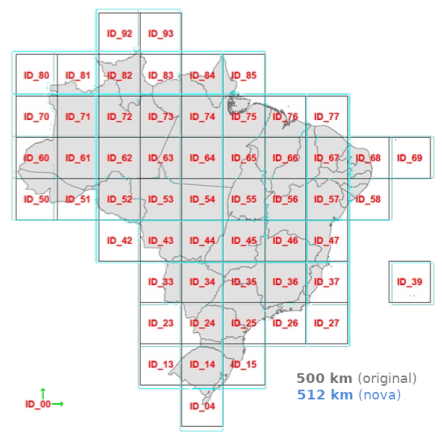
Se fosse o Brasil, necessitaria de uma caixa L0 com lado de h0 = ~5000 km.
A grade oficial brasileira, mantida pelo IBGE, usa um modelo um pouco diferente: definiu um mosaico de ladrilhos cobrindo o território brasileiro e, só depois, estabeleceu que cada um desses ladrilhos da cobertura inicial é que sofre a partição recursiva padronizada (no caso em 25 partes ao invés de 4).
… A Grade Estatística brasileira infelizmente é pouco conhecida e pouco usada, inclusive poucos de nós aqui do Fórum (quem já conhecia levanta a mão!).
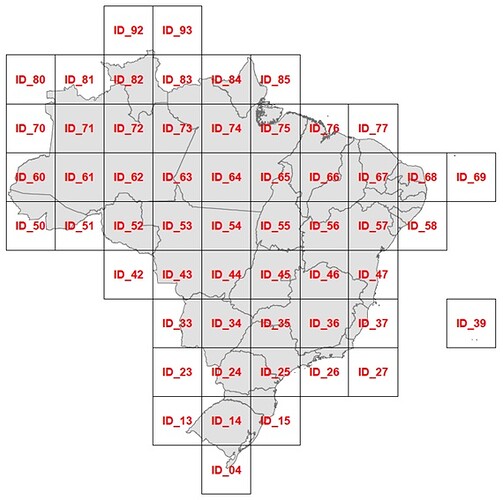
Grade IBGE, a nossa grade
Não é só coisa dos matemáticos estatísticos… Tem até um filminho didático para usar na escola!
O IBGE mantém um repositório estável com a grade em formato shape e dados sobre densidade populacional. É tudo bem acessível:
-
Documento descritivo acadêmico com todos os detalhes (ou procure documento
grade_estatistica.pdfna pasta FTP)
Cidadãos do Brasil, cientistas de dados… Por favor divulguem, usem e abusem da Nossa Grade Estatística!
Essa é a “grade de cobertura” comentada acima. As demais grades, mais refinadas, se originam das partições recursivas, de cada quadrado em 25 quadrados menores. Cada grade portanto pode ser referenciada pelo seu nível L de particao recorrente. É um conjunto padronizado de 7 grades distintas, organizadas por tamanho de lado da célula:
- h0=500 km no nível L0 (seria nível L1 se partissemos da caixa como L0),
- h1=100 km no L1,
- h2=50 km no L2,
- h3=10 km no L3,
- h4=5 km no L4,
- h5=1 km no L5 e
- h6=200 m no L6.
Cada célula da grade de nível L<6 corresponde à união de 25 células de nível L+1.
PS: repare que o Brasil da Ilustracao tem 10 celulas de largura, portanto 10*h0=5000 km de largura, conforme estimado anteriormente.
Na ilustração acima (articulação do L0) percebemos que cada célula, também apelidada de “quadrante”, tem um identificador… Como esse indentificador é um código e pode ser utilizado como localizador (por ex. o município do Chuí fica dentro do quadrante ID_04), dizemos que a grade define um sistema de geocódigos.
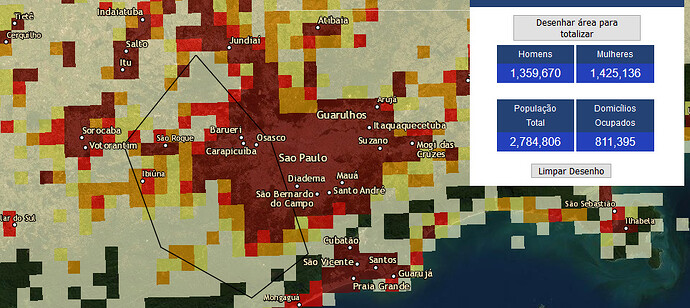
Exemplo de uso.
Acima uma foto da tela da grade interativa, com dados de densidade populacional, disponível em https://mapasinterativos.ibge.gov.br/grade/default.html
A linha poligonal preta fina, envolvendo de Ibiuna até Osasco, serviu de referência para agregar a distribuição populacional, com resultados no quadro azul.
Nomes feios
E para indicar uma célula específica, falar dela, como são os “nomes de célula” (códigos) da grade do IBGE?
Todas as células foram batizadas, e os nomes cumprem seu papel de identificar unívocamente. Por exemplo a célula batizada 100KME5700N8750, da grade do nível L1, representa um quadrante com 10.000 km² de área e 100 km de lado; dentro dela, do nível L2, tem a célula 50KME5750N8750, com 50 km de lado.
Podemos dizer, em matematiquês, que a célula grande contém a pequena, 100KME5700N8750 ⊃ 50KME5750N8750. Esse tipo de relação algébrica espacial existe para todas as células da grade, nas grades dos níveis L1 em diante: toda célula tem mãe na grade de nível L-1. Outros exemplos, expressando uma hierarquia:
1KME5799N8781 ⊂ 5KME5795N8780 ⊂ 10KME5790N8780 ⊂ 50KME5750N8750 ⊂ 100KME5700N8750
Por outro lado, só de bater o olho nestes exemplos já percebemos que são nomes deselegantes, grandalhões. E infelizmente, não dá para “sacar o nome da célula-mãe” só olhando para o nome da célula.
São nomes longos se comparados com o padrão Geohash, que batiza de 6gy a uma célula de 150 km de lado, e dentro dela 6gyc, com ~30km de lado (~700 km²). Ainda comparando, em termos de hierarquia, reparamos que o prefixo 6gy é o rótulo da sua célula-mãe. Algebricante 6gy ⊃ 6gyc. Outros exemplos: 6 ⊃6g ⊃6gy ⊃ 6gyc ⊃ 6gyce ⊃ 6gycex.
Resumindo os problemas com o código de célula do IBGE:
- são muito longos, difíceis de lembrar, a ponto de dificultar a comunicação;
- não são hierárquicos, não identificam os “pais da célula”; as relações algébricas de parentesco não aparecem como relações sintáticas entre prefixos de código.
O problema tem solução, podemos discutir por aqui (!).
Mais usos: porque não uma grade multifinalitária?
Independente dos rótulos de célula serem bonitos ou feios, a Grade Estatística consiste de uma parte da infraestrutura nacional de dados espaciais relevante. Ela pode ser reutilizada em diversos contextos onde há demanda por adoção de um padrão.
Reutilizar em Meio Ambiente, Economia, Saúde, Educação… Até em Logística.
O uso mais popular de um geocódigo nacional, conhecido aqui de todos, talvez seja o CEP dos Correios, que nem sequer é um dado aberto: passaria a ser aberto e mais eficiente.
Hoje inclusive o governo de São Paulo já namora com a Google um substituto mais moderno para o CEP, que seria o PlusCodes. É interessante esse movimento para despertarmos sobre a relevância dos cadastros de endereços postais e tecnologias de localização, para o governo e a iniciativa privada.
É momento de nos mobilizarmos um pouco por padrões abertos, soberania, estudos técnicos, licitação transparentes, etc. É também momento de oferecermos uma alternativa, buscarmos uma solução técnica que atenda a um espectro mais amplo de demandas… Que tal discutir por aqui as alternativas, e uma eventual proposta de CEP baseado na Grade Estatística?